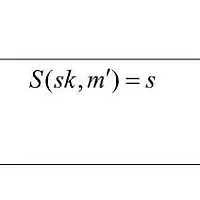대칭키 암호의 문제점
- 새로운 사용자 추가 어려움
- 서로 모르는 사람들끼리 통신하기 위해 키를 받아야함
공개 키 암호의 개념
대칭키에서는 암호화 복호화 키를 모두 같은걸 썼다. 하지만 실제로 사용 하려 할 때는 네트워크로 엮인 수많은 사람이 사용하기 위해선 제한사항이 많다. 대칭키는 공개키와 개인키를 구분하여 문제해결을 제시했다.
공개 키 암호의 성질
- One Way function
y = f(x) 는 쉽지만, x=f(y) 는 어려워야 한다. 복호화가 어려워야 한다.
인수분해와 이산대수의 성질을 이용함
- Trapdoor
부가정보(개인 키) 가 입력이 되면 복호화 하기 쉬워지는 성질.
암호화 과정은 One-way 성질
복호화 과정은 Trapdoor 성질
뭔가 보기만해도 멀미나는 수식이 있는데 결과적으로 의 경우에는 암호화가
의 경우엔 복호화가 된다는걸 말해준다고 한다. p, q 는 소수로 구성되어 n 값을 도출하고 사용자는 p,q 값을 생성하여 자신만이 알고있는 값으로 사용하게 된다. 복호화를 하려면 b 값을 구해야 하는데 b값은 n을 인수분해 하여 p,q 를 구해야만이 알아낼 수 있다. 이러한 인수분해 성질을 이용한 것이 RSA이다.
공개 키 암호의 안전성
- 암호화가 쉽고 키 값을 모를경우 복호화가 어려워야 한다.
- 암호화에서는 전사적 공격에 대응하기 위해 그 크기가 충분히 커야 한다.
- 공개키의 인증문제 : Impersonation attack
신뢰할수 있는 제 3자를 통해 공개키와 인증서를 발급받음으로써 대응
- 공개키 암호의 안전성
Chosen Plaintext Attack 은 항상 가능
Chosen Cipthertext Attack 은 막는다.
knapsack Algorithm
knapsack은 배낭이라는 뜻이다. 배낭안에 물건을 차곡차곡 넣어 꺼내쓰는것 처럼 super-increase의 순서대로 나열된 수열을 넣고 키값을 생성 한다. super-increasing 은 다음에 올 수의 값이 같은값이 아닌 무조건 1이상 높은 수가 와야 한다는 규칙.
super-increasing sequence : [2,3,6,13,27,52] 가 있다고 하자. 이것이 개인키가 된다. |
이때 multiplier 로서 n을 정하고 moduler로서 m 을 정해야 한다.
n과 m의 관계는
m > total( 수열의 모든 합 ) , gcd(m,n)= 1 (서로 소) 의 관계가 되어야 한다. m = 105 , n = 31 로 정했다. |
각 수열에 n을 곱하고 mod m 을 연산한다.
2 * 31 mod 105 = 64 3 * 31 mod 105 = 93 6 * 31 mod 105 = 81 13 * 31 mod 105 = 88 27 * 31 mod 105 = 102 52 * 31 mod 105 = 37 | 연산된 결과는 공개 키가 된다. | public key : [64, 93, 81, 88, 102, 37] |
이제 공개키를 암호화 한다.
메세지 : 011000 110101 101110 가 주어졌다. |
암호화는 주어진 메세지(index 역활)와 공개키를 이용해서 생성한다.
011000 은 6개의 수열 요소중 93, 81을 가리킨다. 이들을 모두 더하면 암호문(Ciphertext)가 만들어진다.
011000 = 93 + 81 = 174
110101 = 64 + 93 + 88 + 37 = 280
101110 = 64 + 81 + 88 + 102 = 333 으로 Ciphertext = [174, 280, 333]이 된다.
이를 복호화하려면 어떻게 해야할까
개인 키 값을 가지고 찾아 낼 수있다.
암호문에 특정한 수를 곱해줘야 하는데 그 수는
multiplier(n) * x mod moduler(m) = 1 에서 x를 구해야 한다. 어떤연산을 했을때 항등원이 나오는 역원을 구한다. (항등원은 어떤수를 연떤 연산을 했을 때 자기 자신이 나오는것) |
31 * x mod 105 = 1 이 되는 경우는 61이 있다. 이제 x=61로 대입해 암호문을 복호화 해보자.
복호화는 위의 공식과 비슷하게
Ciphertext * 61 mod m 으로 연산하고 결과값을 개인키에서 찾는다. |
private key = [2,3,6,13,27,52]
===================
174*61 mod 105 = 9 = 3+6
280*61 mod 105 = 70 = 2+3+13+52
333*62 mod 105 = 48 = 2+6+13+27
RSA(Rivest-Shamir-Adleman)
인수분해의 one-way 특성을 이용해 키를 사용한다.
- 키생성
1. 비슷한 크기의 두 소수를 구한다. (p ,q) (전사적 공격에 대응하기위해서는 값이 커야겠지?)
2. n = pd , ∮(n) = (p-1)(q-1) 을 계산
3. gcd(e, ∮(n)) = 1 ( ∮(n)과 최대공약수가 1뿐인 e)을 만족하는 e 선택
4. e*d = 1 mod ∮(n) 를 만족하는 d 계산
공개키 (e, n) 개인키 (d,p,q)
암호화 과정은 메세지에 공개키를 사용해서 만든다.
복호화 과정은 암호문에 개인키 d 를 사용해서 복호화 한다.
안전성
1. n을 인수분해 하면 RSA는 해독 됨 → d 값을 알아낼 수있다. 하지만 인수분해 하기 어렵다
2. e,d,n의 문제 - e 값이 작을경우 CRT에 의해 공략 될 수 있다. → salting 기법으로 대응 (난수 첨가)
3. p, q 의 값이 충분히 크고 차이가 크지 않아야 한다. → 차이가 클 경우 타원 곡선을 이용한 인수분해가 가능하다
'Kitri_NCS3기 보안과정 > 정보보호개론' 카테고리의 다른 글
| 170329 키 관리 (0) | 2017.03.29 |
|---|---|
| 170329 전자서명 (0) | 2017.03.29 |
| 170328 해쉬함수 (0) | 2017.03.28 |
| 170327 블록암호화 DES (0) | 2017.03.27 |
| 170327 고전 암호 기법 (0) | 2017.03.27 |